Obliczenia
Obliczenia dla pojedyńczej sprężyny talerzowej
Obliczenia zakładają, że podczas ugięcia powierzchnia boczna sprężyny obraca się wokół środka obrotu, znajdującego się na środku powierzchni bocznej sprężyny talerzowej o średnicy D0.
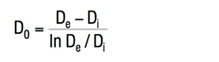
Wzór 1
Obrót przekroju poprzecznego stanowi źródło różnych naprężeń i zjawiska sprężynowania.
Obliczenia zakładają, że moduł sprężystości wzdłużnej „E” pozostaje liniowy dla danego materiału, przekrój sprężyny jest prostokątny o ostrych narożnikach, a podczas ugięcia sprężyna talerzowa pozostaje w jednej płaszczyźnie. Obciążenie przykładane jest w punktach I i III. Naprężenie szczątkowe występujące w sprężynie po jej wytworzeniu i obróbce cieplnej można pominąć.
Pomimo, że obecnie dostępne są bardziej precyzyjne metody obliczeń [10] [12] [13] nie ma powodu, by zaniechać stosowania prostych i wygodnych wzorów normy DIN 2092. Dla wymiarów standardowych dają one bowiem wartości bardzo zbliżone do wyników pomiarowych.
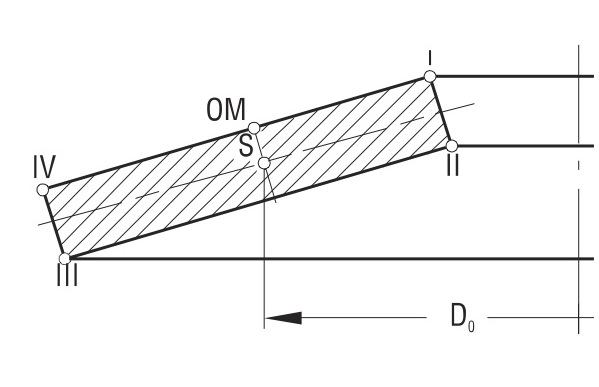
Rys. 1
Położenie środka obrotu i punktu OM.
Równania do obliczeń
Poniższe obowiązuje dla wszystkich sprężyn talerzowych:
Charakterystyka
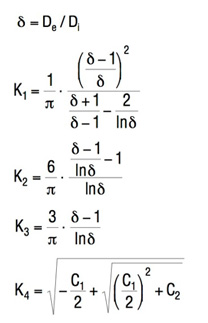
Wzór 3
Wzór 4
Wzór 5
Wzór 6 gdzie a
Siła nacisku sprężyny talerzowej
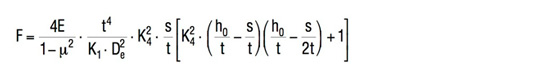
Wzór 7
Dla sprężyn talerzowych produkowanych w grupach 1 i 2 K4 = 1:
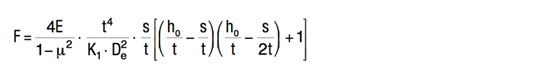
Wzór 8a
Dla sprężyn talerzowych produkowanych w grupie 3 z płaskimi powierzchniami
stykowymi i o zmniejszonej grubości t’ i h0′ należy stosować (h0′ = l0 – t’):
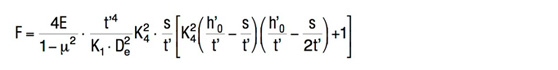
Wzór 8b
W przypadku sprężyn talerzowych stalowych o wymiarach zgodnych z DIN 2093, wzór 7 daje wyniki bardzo zbliżone do wartości pomiarowych.
Siła nacisku sprężyny talerzowej nie wzrasta liniowo wraz z ugięciem, lecz jest zakrzywiona wstecznie. Jej wysokość tj. sztywność maleje wraz ze wzrostem skoku. Wielkość krzywizny wyznaczona jest wyłącznie przez współczynnik h0/t jak to przedstawia rys. 2.
Obliczenia naprężeń sprężyny talerzowej DIN 2093
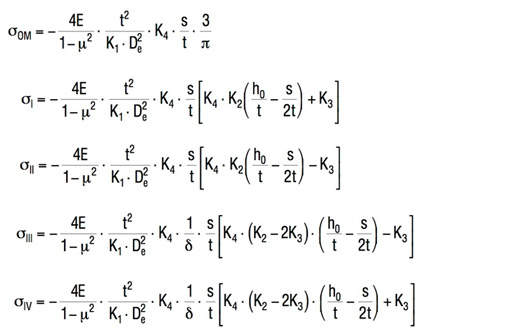
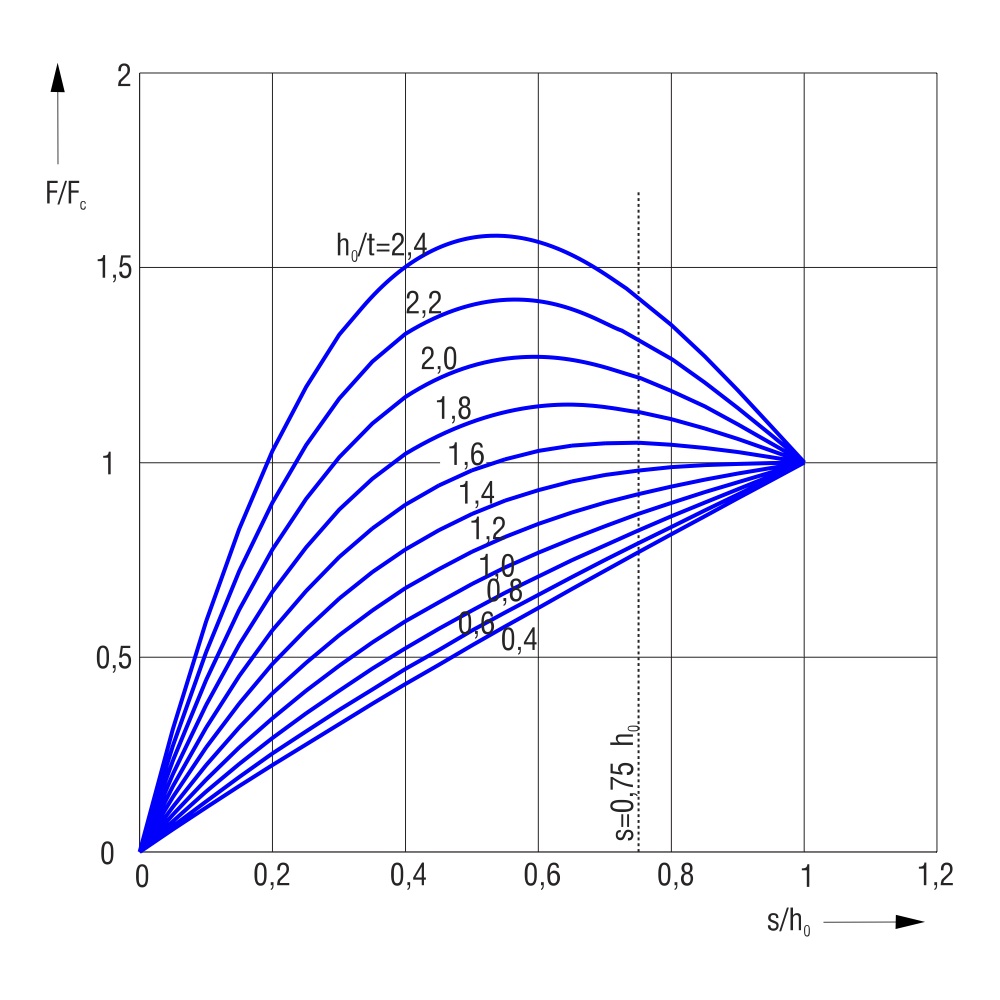
Rys. 2
Krzywa charakterystyki sprężyny względem h0/t i s/h0.
Tutaj:
odnosi się również do stali sprężynowej. Wartości dodatnie oznaczają wytrzymałość na rozciąganie, zaś wartości ujemne – naprężenie ściskające. Należy
pamiętać, że tak obliczone naprężenie stanowi wartość nominalną, zaś naprężenie rzeczywiste jest znacznie niższe, ponieważ w znacznym stopniu oddziałuje na nie stale obecne naprężenie wewnętrzne.
Ugięcie właściwe sprężyny
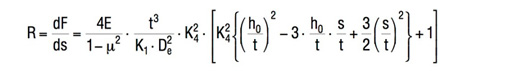
Poprzez różnicowanie obciążenia sprężyny F zgodnie z ugięciem s, uzyskuje się poniższy wzór na ugięcie właściwe sprężyny R:
Wzór 14
Ugięcie właściwe sprężyny pomiędzy dwoma przyległymi punktami F1, s1 i F2, s2 można w przybliżeniu obliczyć za pomocą poniższego, prostego wzoru:
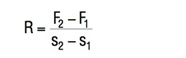
Wzór 15
Praca sprężyny talerzowej
Wartość pracy wykonywanej przez sprężynę można uzyskać z wzoru całkującego 7 dla obciążenia F przy ugięciu s:
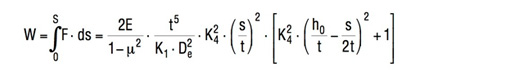
Wzór 16
Dla ograniczonego obszaru zastosowań całkowanie można ograniczyć do zakresu pomiędzy dwoma ugięciami s1 i s2.
Sprężyny talerzowe bez płaskich powierzchni stykowych
Ze względu na przekrój prostokątny o zaokrąglonych narożach, zgodnie ze specyfikacją sprężyn z grup 1 i 2, przyłożenie obciążenia w praktyce zawsze odbywa się za pośrednictwem nieznacznie skróconych ramion dźwigni (Rys. 3). Z uwagi na tolerancję h/H dla średnicy zewnętrznej i wewnętrznej, ramiona dźwigni są jeszcze bardziej skrócone. Powoduje to zwiększenie obciążenia sprężyny o współczynnik:
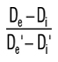
w przypadku praktycznie wszystkich sprężyn w porównaniu z wartościami obliczonymi za pomocą wzoru 7.
Warunki takie uwzględnia norma DIN 2093, gdzie ujemne tolerancje grubości są znacznie większe od tolerancji dodatnich. Dlatego niektóre produkowane przez nas sprężyny talerzowe posiadają nieznacznie zmniejszoną grubość krążka. To zmniejszenie długości ramienia dźwigni stanowi również wyjaśnienie, dlaczego dopuszczalne odchylenia obciążeń sprężyny dla grup 1 i 2 są znacząco wyższe w kierunku dodatnim niż w kierunku ujemnym.
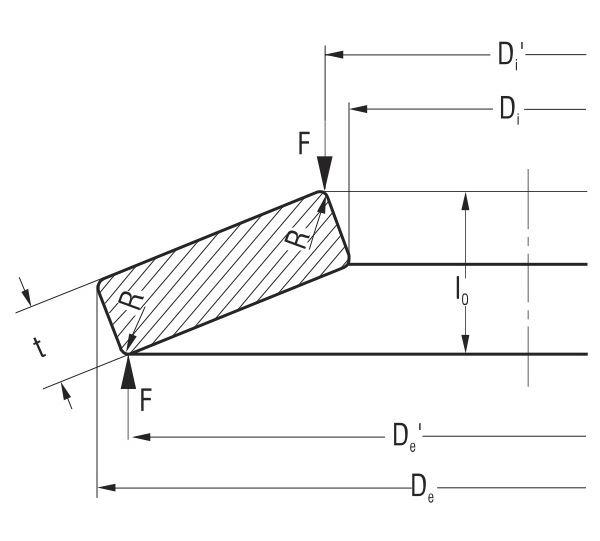
Rys. 3
Przekrój sprężyny talerzowej w grupie 2





